Sonsuzluk – 8

Uzun bir aradan sonra Sonsuzluk ifadesin matematiksel ifadelerine bu yazı ile geri döneceğiz. Yazımıza bir soru ile başlayıp sorunun açılımı ile devam edeceğiz

“Rahmetim gazabımı geçti.

Hadis-i Şerif

Hem Allah sonsuz deniliyor hem de Rahmeti sonsuzdur deniliyor. Öyle ki iki tane sonsuz olmaz, ayrıca Rahmeti sonsuz ise Gazabının durumu nedir? Gazabı sonlu mudur yoksa Gazabı da sonsuz mudur? Eğer Gazabı da sonsuz ise Rahmet nasıl olur da Gazabı geçebilir, bu müşkildir. Yok Gazabı sonlu ise bu acizlik değil midir?

Bu sorular ilk yazılarımızda bahsettiğimiz sonsuz tanımı göze alınmadığında haklı ve içinden çıkılamayacak sorular gibi duruyor. İki tane sonsuz varsa birbirlerini dışlarlar. Sonsuz bir tane olmalıdır.

Soruyu irdelemeye başlamadan önce bazı kavramları hatırlatmak faydalı olacaktır. Sonsuz, ifade edilemez, sınır koyulamaz, başı ve sonu yoktur. Eğer başı, sonu olursa bu onu sınırlı yapar demiştik.

Buna ek olarak sayı doğrusu sonsuza gitmez, sayı doğrusunun durumu sınırı belirsizce artandır. Aynı zamanda sonsuzluk yürüyerek veyahut biriktirilerek ulaşılabilecek bir şey de değildir. Sayı doğrusu ile ilgili son hatırlatmamızı yaparak konumuza girelim. Sayı doğrusunda sıfır ile bir arasında da sonsuz sayı değil sayılamayacak kadar çok sayı vardır. 

Bu kavramlardan sonra şunu söyleyebiliriz. Hakiki SONSUZ tektir. Diğerleri sonsuz değildir. Bu durumu kavramlaştırma adına Tolkien’den mülhem bir kavram getireceğiz. Tolkien yaratma kavramının sadece Eru’ya ait olduğunu ve bu sebeple creat(yaratma) kavramının sadece O’na ait olduğunu belirtir. Vaların durumu için ise sub-create (alt yaratı) kavramını önerir. Biz de bu kavramlaştırmadan yola çıkarak, hakiki sonsuz bir tanedir, dolayısı ile diğer kavramlar sonsuz değildir, sonsuz dışındaki diğerler ifadeler için alt-sonsuz kavramını kullanacağız. Bu yazıda geçen bütün sonsuz kelimelerini alt-sonsuz olarak anlamanızı istirham ediyoruz. Anlatımı kolaylaştırma adına bu şekilde yazı içerisinde alt-sonsuz kelimesi yerine  sonsuz kelimesini kullanmayı uygun gördük.

Kardinal ve Ordinal Sayılar

Kardinal sayılar bir gruptaki öğe sayısını belirten sayılardır yani kaç tane sorusunun cevabıdır. Ordinal sayılar ise bir sıradaki öğenin yerini belirten sayıdır ve kaçıncı sorusunun cevabıdır. Kardinal Sayılara örnek kasadaki 5 portakal, raftaki 3 elma iken Ordinal sayı örneği ise yarışmada birinci gelen, 5. sırada olan kişidir.

ORDİNALLER VE KARDİNALLER

İlk yüz pozitif tam sayının kaçı tam karedir? Bu sayılar 1,4, 9, 16, 25, 36, 49, 64, 81 ve 100 olduğuna göre 10’u. Demek ki ilk yüz pozitif tam sayının %10’u tam karedir, Peki ilk bin pozitif tam sayının yüzde kaçı tam karedir? 31’in karesi 961, 32’nin karesi 1024 olduğuna göre, 31 tanesi, yani %3,1’i. İlk on bin pozitif tam sayının ise %1’i tam karedir, zira on binin karekökü yüzdür. İlk n pozitif tam sayının içindeki tam kare sayıların adedine m dersek (m, karekök n’e eşit ya da küçük en büyük tam sayıdır), oranı, n büyüdükçe azalır, zira tam sayılar büyüdükçe, kendileri ile kareleri arasındaki mesafe açılır. Hatta n sonsuza giderken bu oran sıfıra yaklaşır.

Bu akıl yürütmeyi burada bırakıp şimdi başka bir akıl yürütmeye geçelim. Pozitif tam sayıları ki bunlara sayma sayıları ya da doğal sayılar da denir, 1’den başlayarak, sırayla ve hiçbirini tekrar etmeden, aşağıdaki gibi, bir satıra yazalım. Sonra bu sayıların karelerini, her sayının karesi kendi altına gelecek şekilde ikinci satıra yazalım.

1 2 3 4    5  6   7   8   9   10 …

1 4 9 16 25 36 49 64 81 100 …

Bu iki satırdan üsttekine, doğal sayı dizisi D (bu kitapta 0’ı doğal sayılar kümesine dahil etmiyoruz), alttakine tam kare sayı dizisi K diyelim. D ve K dizilerinin elemanlarını sırasıyla d₁, d2, …, dn … ve k₁, k2, k3…, kn,… notasyonlarıyla gösterelim. D’nin her di elemanına, K’da bir ki elemanı karşılık gelir, zira karesi olmayan bir doğal sayı yoktur. Yani, D’deki sayılar, hem D hem de K dizilerinin elemanlarını sayarlar. Dolayısıyla n bir doğal sayı olmak üzere sonsuza doğru giderken D ve K dizilerinin eleman sayılarının oranı değişmez ve hep 1 olarak kalır.

Bu iki akıl yürütmenin ikisi de çok sağlam olmasına rağmen birbirleriyle çelişiyor gibi görünen sonuçlar ima ederler, zira birinci akıl yürütme, tam kare sayılardan çok daha fazla doğal sayı olduğunu işaret ederken ikinci akıl yürütme bu dizilerin eleman sayılarının eşit olduğunu telkin etmektedir. n² sonlu olduğunda, yani D ve K dizileri belli bir sayıda sonlandığında, herhangi bir çelişki doğmaz, zira n sonlu, belli ve sabit ise n² de sonlu, belli ve sabittir. İlk n tam kare sayıdan oluşan sonlu bir diziye, ilk n² doğal sayıdan oluşan başka bir sonlu dizi eşlik eder ve bu dizilerin ilkinde n, ikincisinde n² sayıda eleman vardır. Çelişki n sonsuza giderken, ya da böyle söylemeyi tercih ediyorsanız, n sonsuz olduğunda ortaya çıkmaktadır.

Peki o zaman, bu birinci akıl yürütmedeki kıyasın ulaştığı sonucun anlamı nedir? Bu akıl yürütmede kıyaslanan şeylerin, söz konusu dizilerin büyüme hızları olduğu söylenebilir. Bunun daha iyi anlaşılabilmesi için K ve D dizilerindeki kutuların birer lamba olduğunu düşünelim. K’daki her lamba, bir iletken telle D’nin bir lambasına bağlansın (lambalar bu yolla birebir eşleştirilsin). Dolayısıyla dizilerin birinde herhangi bir lamba yandığında diğer dizideki eşlenik lamba da yanıyor olsun. Dizilerin lambaları arasındaki bağlantıları f(n) = n² bağıntısına uyacak şekilde yapalım, yani K’nın n’inci lambasını, D’nin n²”ninci lambasına bağlayalım. Bu eşleştirme, K ve D dizileri arasında ordinal değil, kardinal bir eşleştirmedir. Son olarak bir de dizilerde herhangi bir lamba yandığı zaman, kendinden önceki tüm lambaların da yanmasını sağlıyor olsun. Şimdi, K dizisinin lambalarını sırayla, örneğin her saniye bir sonraki yanacak şekilde yakmaya başlayalım. K’nın n’inci lambasını yaktığımız anda, D’nin n2’ninci lambası da yanar. Bunun anlamı şudur: n’inci tam kare sayıdan söz etmek, aslında n2’ninci doğal sayıdan da söz etmek emektir. Öyleyse n/n2 oranının, K dizisinin D dizisine göre bağıl büyüme hızı olduğu söylenebilir. K dizisi üzerinde hangi hızla ilerlerseniz, D dizisi üzerinde o hızının katı kadar bir hızla ilerlemiş olursunuz. Başka bir deyişle, kare kare saymak, tek tek saymanın n katı kadar yavaştır. n büyüdükçe bu hızlar arasındaki fark da büyür. Söz konusu fark, n sonsuza giderken o kadar açılır ki D dizisinin ilerleyişine nazaran K dizisi durmuş gibi görünür. Her iki akıl yürütmeyi de kapsayacak şekilde daha hassas bir biçimde ifade edecek olursak, K ve D dizileri, ordinal eşleşmede aynı hızla büyürken kardinal eşleşmede farklı hızlarda büyürler.

Sonlu bir küme, bir başka kümeyi kapsadığında, alt kümenin eleman sayısı üst kümenin eleman sayısından az olur (alt ve üst kümelerin aynı küme olmadığını varsayıyoruz). Bu alışkanlık, bizi, aynı şeyin sonsuz kümelerde de geçerli olduğu düşüncesine sürüklemektedir. Halbuki böyle bir sonuca ulaşmak, üzerinde yeterince düşünülmeden verilmiş bir karar olur, zira sonsuz kümelerde sayısız eleman vardır. Tam kare sayılar, doğal sayıların bir alt kümesidir, yani doğal sayılar, tam kare sayıları kapsar. Ancak bu gerçek, doğal sayıların sayısının tam kare sayıların sayısıyla, doğal sayılar kümesi, tam kare sayılar kümesinden kapsama bakımından büyük olmasına (D ⊃ K) rağmen, eleman sayısı bakımından büyük değildir . Bununla birlikte bu iki kümenin aynı sayıda elemana sahip olduğunu söylemek de doğru olmaz, zira her iki kümede de sonlu ve belli bir sayıda değil, belirsiz çoklukta eleman mevcuttur.

Yazının başında sormuş olduğumuz Rahmet Gazabı nasıl geçer sorusunun cevabını bu şekilde vermiş oluruz. Zira doğal sayılar kümesi,  tam kare sayı kümesini kapsama bakımından büyüktür. Bu iki tane sınırı belirsizin karşılaştırması ve arasında bir hiyerarşi olduğunu bize gösterir. Dolayısıyla Rahmetin Gazabı geçmesi konusu bu şekilde açıklığa kavuşmuş gibi görünüyor. Aslında bu kusurlu bir ifadedir. Konuyu daha fazla açmamakla beraber burada bir şekilde sayıların sayısı olmaması gibi yani bir son sayı olmaması gibi alt-sonsuzlarda da böyle bir mevcut olur ki bu durumda Rahmet geçer derken onu Gazaba kıyasla daha alt bir konuma koymuş oluruz. Doğal sayılar kümesinin alt kümelerinden oluşan güç kümesi, doğal sayılar kümesinden daha büyüktür. Yani doğal sayılar kümesinin büyüklüğünden daha büyük bir büyüklük vardır. Bu sonsuz büyüklüklerin kendi içinde farklı seviyelerde olduğunu, tüm  sonsuzlukların aynı seviyede olmadığını gösterir. Buradaki anlatım yayılma ile ilgilidir. Bu yayılma ile ilgili kısmı ileride çizgi kare anolojisi üzerinden  tekrar anlatacağız. 

SONSUZ DİZİLERİN AÇIK VE KAPALI TASAVVURLARI

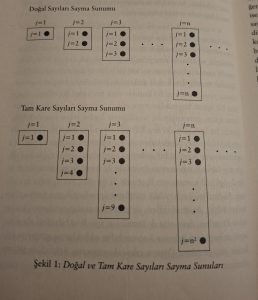
Yukarıda verilen fiziksel senaryodaki kutular, içine istediğiniz sayıda eleman koyabileceğiniz ve bu elemanları çerçeveleyerek bir birlik haline getiren yapıları, bilyeler ise kendisine bir şey ekleyip çıkaramayacağımız birimleri, yani daha fazla genişletemeyeceğimiz (ya da daha kök hale getiremeyeceğimiz) saf sayılabilirliği temsil eder. Doğal sayı dizisini gerek bilyelerle gerekse kutularla temsil etmek mümkündür. Bilyeleri veya boş kutuları yan yana dizip üzerlerine birer birer artan sıra numaraları yazdığımızda doğal sayı dizisini fiziksel olarak temsil etmiş oluruz.

Dolayısıyla, Şekil 1’in üst panelinde verilen doğal sayıları sayma sunumunda gerek kutular gerekse bilyeler, doğal sayıları say-maktadır. Bu sunumda bir “son” kutu çizebilseydik, o kutunun içine sayısız bilye koymamız gerekirdi ve bu “son” kutu, doğal sayı dizisini kapalı bir biçimde temsil etmiş olurdu. Bununla birlikte yan yana dizili kutular ise aynı doğal sayı dizisini açık bir biçimde temsil etmektedir (Şekil 2’ye bakınız). Şekil 1’in alt panelinde verilen tam kare sayıları sayma sunumunda çizilebilecek bir “son” kutu da doğal sayıları sayma sunumundaki “son” kutunun aynısı olacaktı. Dolayısıyla, bu ikinci sunumdaki kutular, tam kare sayı dizisini açık tarzda temsil ederken, tahayyül ettiğimiz “son” kutu, doğal sayı dizisini kapalı tarzda temsil etmiş olurdu. Sonsuz bir diziyi, bir ucu açık olarak düşündüğümüzde dizinin sonsuzluğunu bilkuvve bir sonsuzluk olarak tasavvur etmiş oluruz; aynı diziyi kapalı bir kutunun içindeymiş gibi düşündüğümüzde ise dizinin sonsuzluğunu bilfiil bir sonsuzluk olarak tasavvur etmiş oluruz.

Bir grup sayı, kapalı bir şekilde sunulduğunda, tek bir eleman gibi düşünülebilecek bir birlik oluşturur ve bu birliği, o sayıları çerçeveleyen kutu temsil eder. Kutular, içlerine yerleştirilen sayıların sayısının bir önemi olmaksızın, hepsinin topluca tek bir eleman gibi sayılmasını sağlar. Yukarıda bahsettiğimiz, ikinci akıl yürütmede tüm birebir örten f(n) fonksiyonlarının, f(n) = n’e dönüşmesinin nedeni, işte bu kutulama (birleme), yani bir grup sayının bir birlik hâline getirilmesi, başka bir deyişle söz konusu sayıların kapalı olarak tasavvur edilmesidir.

Sonlu dizilerin açık tasavvurundan söz etmek anlamsızdır, zira bu dizilerin son elemanları, onları zaten kapatır ve bu iş için ayrıca bir kutuya gerek duyulmaz. Bu, tüm sonlu sayıların kapalı olduğu anlamına gelir. Sonsuz dizilerin bir son elemanı olmadığından doğal olan tutum bu dizileri açık tasavvur etmektir. Sonsuzluk böyle doğal ve açık bir biçimde tasavvur edildiğinde, bilfiil ulaşılabilen, gerçekleşebilen, tüketilebilen, tamamlanmış, değişmeyen, belli ve tüm parçaları sabit bir şey olarak değil, kendisine sadece yaklaşılabilen ama hiçbir zaman tüketilemeyen, potansiyel bir gerçeklik olarak anlaşılır. Bu nedenle sonsuz diziler, tamamlanmamış bir süreç olarak görülür. Belli bir son elemanı olmayan dizilerin, sonlu, yani kapalı bir eleman sayısı da yoktur. Bu tasavvurda tüm doğal sayılar, sonlu, belli ve sabittir; herhangi bir doğal sayıya, sonlu sayıda adımla ulaşılır; doğal sayı olmak, sonlu (kapalı), belli ve sabit olmakla eş anlamlıdır. Dolayısıyla sonsuzluğu bu tasavvurda, literal anlamda sayısız olmakla tarif eder ve söz gelimi, “sayısız doğal sayı vardır” deriz. Bu, sonsuzun, sadece sonlu bir sayı olmadığı değil, “sonsuz sayı” diye bir şeyin de olmadığı, başka bir deyişle, sonsuzluğun bir sayı olmadığı anlamına gelir. Öte yandan sonsuz bir dizinin, kapalı bir biçimde tasavvur edilebileceği de düşünülebilir. Bu durumda söz konusu dizinin, her ne kadar belli bir son elemana sahip olmasa da kapalı bir küme olduğu varsayılır, zira bu kümenin, başka kümelerden ayırt edilebilme anlamında ne olduğu bellidir; kümenin bir son elemanı olmasa bile bir sınırı ve limiti vardır. Yani bu sonsuz kümeyi, içindeki “son” elemanı değil, dışındaki limit kapatır (sonlu kümeler içeriden, sonsuz kümeler dışarıdan kapalıdır denebilir). Bun tasavvurda sonsuzluk, bilfiil ulaşılabilen, tamamlanabilen, tüketilebilen, değişmeyen, belli ve tüm parçaları sabit bir limit olarak görülür. Dolayısıyla, sonsuz kümelerin, sonlu olmayan ama kapalı bir eleman sayısı vardır, zira artık kapalı olmakla sonlu olmak eş anlamlı değildir. Bu, sonsuzluğun bir yandan tamamlanmış, değişmeyen ve belli bir sayı olarak düşünülmesi, diğer yandan ise sonlu bir değer atanamaması anlamına gelir. Söz gelimi “sonsuz sayıda doğal sayı vardır” dediğimizde, bilerek ya da bilmeyerek, bir sonsuz sayıdan bahsetmiş oluruz. Bu yüzden, bu tasavvurda, sonlu sayılardan oldukça farklı özellikler gösterdikleri için başka bir tür sayı oldukları söylenen sonluötesi (transfinite) sayılar tasarlanmıştır.

Mutlak Gerçek ve Sonsuz İmkan- Ali Sebetci

Yorum

Burada sonsuz dizinin iki türlü gösterimi mevcut açık ve kapalı olma durumu. Buradaki durumu kendi yazı dizimizin konusu olan Rahmet üzerinden bir açıklama getirebiliriz. Rahmet kelimesinin Arapçada iki türlü yazımı vardır. Açık T harfi ve kapalı T harfi ile.

Tâ-i Meftûha (Açık “t”)
Yazımı: ت
Kullanımı: Genellikle fiillerde ve kelime içindeki “t” sesini temsil eder.
İşlevi: Kelime sonunda, “tâ-i merbûta” (ة) gibi, kelimeye “dişilik” (müenneslik) anlamı katabilir; ancak yazımı ve telaffuzu farklıdır.
Önemli Not: Kur’an-ı Kerim’in bazı yazımlarında, gramer kurallarına aykırı olarak, açık “tâ”nın kelime sonunda kullanıldığı görülebilir.
Tâ-i Merbûta (Kapalı “t”)
Yazımı: ة
Kullanımı: Sadece kelime sonlarında, bir ismin “dişi” (müennes) olduğuna işaret etmek için kullanılır.
İşlevi: İsmin cinsiyetini belirtir.
Önemli Not: “Tâ-i merbûta” kelime sonunda ek olarak gelir ve kelimenin kendisiyle birleşir.

Arapça dil bilgisine haiz değiliz lakin bu iki fark bizlere Rahmetin iki türlü durumundan haber veriyor olabilir. Biri tecelli etmemiş hali, diğeri ise tecelli etmiş hali gibi. Biri being seviyesindeki durumu (bilkuvve) diğeri ise existence seviyesindeki durumu gibi. Zira existence durumunda tecelli etmiş ve kapalı bir hal almıştır. Bu kapalı hal sonsuz dizinin kapalı tasavvurundaki kapalı haldir. Örnek verecek olursak Sonsuz Rahmet kainatta tecelli etti. Burada kainat sınırları olan kapalı bir alandır buna rağmen içerisinde yine sonsuz çokluk olan bir yerdir ama  aynı zamanda da bir kapalılık ifade eder.

Rahmetim her şeyi kuşatmıştır. (küçük not buradaki ayette açık t harfi kullanılmıştır.)

Araf Suresi-156. ayet

Rahman arşa istiva etti.

Taha Suresi- 5. Ayet

Bu yayılımın aşağısında daha alt-sonsuzlar da mevcuttur. Buna örnek olarak nimetlerini saymaya kalsanız saymaya gücünüz yetmez ayeti gösterilebilir. Zira nimetleri sayılamayacak kadar çoktur. Örnek olarak 0 ile 1 arasındaki sayıları saymaya kalkışmak, tüketilebilen bir şey değildir. Peki bunca sonsuz nimetin şükrü nasıl eda edilir denilirse sonsuz bir şükür niyeti ile eda edilebilir bu da aslında yukarıda yazı içinde belirtildiği gibi sonsuz kümeyi, içindeki son eleman değil, dışındaki limit kapatır, yani sonsuz şükür hissi, bir nevi limit alma işlemi gibi düşünülebilir.

Bu yazıdaki sonsuzluk kavramlarının hepsinin Sonsuz değil İzafi Sonsuz olduğunu belirtip, Tolkien’den mülhem alt-sonsuz demiştik. Bu yayılımı ifade ederken şu örnek de bize açıklayıcı olacaktır. Mutlak’ın sembolü noktadır. Noktaların yan yana  gelmesi ile düz bir çizgi elde etmiş oluruz. Çizgide kaç nokta var denilecek olursa sayılamayacak kadar çok nokta vardır. Yayılımı devam ettirirsek çizgilerin yan yana gelmesi ile alan/kare elde etmiş oluruz. Aynı soruyu burada tekrar soracak olursak, alanın içinde kaç adet çizgi vardır? Cevabımız yine sayılamayacak kadar çok olur. Yayılımı daha da devam ettirerek kareleri yan yana getirdiğimizde küp şeklini elde ederiz. Sorumuzu bir kez daha yineleyelim ve küpün içinde kaç kare vardır? Cevap yine değişmiyor. Burada görmüş olduğumuz gibi her tecelli boyutu/varlık mertebesi aşağı doğru gittikçe belirlenim / sınır kazanıyor aynı zamanda kesrete doğru da bir yolculuk oluyor. Varlık mertebesinde aşağıdan yukarı doğru gidildiğinde eksilme mevcutken ayrı zamanda kaynağa yaklaşma oluyor. Bu eksilmeyi tenzih etme ile bağdaştırabiliriz. Varlık mertebelerinin en altından yukarı mertebelere ait sorularda mantık hatası olan sorularla karşılaşıyoruz. Bunu küp örneği üzerinden soracak olursak düz çizginin yüksekliği nasıldır denilirse bu hatalı bir soru olacaktır zira düz çizginin kendi mertebesinde yükseklik mevzu bahis değildir. Bu aynı şekilde Tanrı’nın şekli var mıdır türünden sorularda da geçerlidir. Yazının başında bahsi geçen hem Rahmet sonsuz hem Gazabı sonsuz önermesi de böyle bir mantık hatası içermektedir. Zira Sonsuzluk Zat mertebesinedir. İsimler ise izafi/alt sonsuzluklardır. Rahmetin Gazabı geçmesi durumu ise yaylım ile bilkuvve içerme ile açıklanabilir. Yani doğal sayılardaki bütün sayıların kaynağı 1’dir. Yayılım oradan gerçekleşir. Dolayısıyla Rahmet Gazabı geçmiş olur.

Not: Yazımızda matematiksel ifadeler ve ispatlar kullanmaktan beri  durmamızın sebebi yazının anlaşılabilirliğini ön planda tutma gayretimiz oldu. Konu oldukça geniş ve derin olmakla birlikte toparlayıp anlatılabilmesi de hayli müşkül olmakta. Bu sebeple bir çok konuyu atladık veyahut hiç değinmedik. Bu sebeple merak edenler için yapabileceğiniz şey ancak kitap tavsiyesi olacaktır. Guenon’un Sonsuz Küçükler Hesabı ve Ali Sebetci’nin Mutlak Gerçek ve Sonsuz İmkan kitabına bakılabilir. Ek olarak aşağıdaki Youtube videosunda Cantor’un teoremi ile ilgili anlatımına göz gezdirilebilir. 

https://www.youtube.com/watch?v=43XC6rAXs-8

Bir sonraki yazımızda ele alacağımız konu “Ben göklere yere sığmadım. Mümin kulumun kalbine sığdım”.